NumPyの使い方(ndarray, random, ブロードキャストなど)

2022/11/26

numpyは、多次元配列を扱う数値演算ライブラリです。ここでは、numpyをインストールして基本的な操作方法を確認します。

インストール

pipenv を利用している場合、以下のようにインストールします。

$ pipenv install numpy

プログラムから利用するにはimportが必要です。
慣習的にnumpyをimportするときは np と別名をつけます。

import numpy as np

print(np.array([0, 1, 2]))  # [0 1 2]

ndarrayオブジェクトの生成

ndarrayオブジェクト

numpyは ndarray というクラスを扱います。

numpyの arrayメソッド の戻り値は、 ndarrayクラス のオブジェクトになります。

>>> print(np.array([0, 1, 2]).__class__.__name__)
ndarray

help関数 で ndarrayクラス の説明を確認できます。

help(np.array([0, 1, 2]))

array｜一次元配列

>>> np.array([0, 1, 2])
array([0, 1, 2])

array｜二次元配列

>>> np.array([[0, 1, 2], [3, 4, 5]])
array([[0, 1, 2],
       [3, 4, 5]])

array｜三次元配列

>>> np.array([[[0, 1, 2], [3, 4, 5]], [[6, 7, 8], [8, 9, 10]]])
array([[[ 0,  1,  2],
        [ 3,  4,  5]],

       [[ 6,  7,  8],
        [ 8,  9, 10]]])

zeros｜0で初期化されたndarray

>>> np.zeros((3, 4))
array([[0., 0., 0., 0.],
       [0., 0., 0., 0.],
       [0., 0., 0., 0.]])
>>> 
>>> np.zeros((3, 4), dtype=np.int16)
array([[0, 0, 0, 0],
       [0, 0, 0, 0],
       [0, 0, 0, 0]], dtype=int16)

ones｜1で初期化されたndarray

>>> np.ones((3, 4))
array([[1., 1., 1., 1.],
       [1., 1., 1., 1.],
       [1., 1., 1., 1.]])
>>> 
>>> np.ones((3, 4), dtype=np.int16)
array([[1, 1, 1, 1],
       [1, 1, 1, 1],
       [1, 1, 1, 1]], dtype=int16)

arange｜連番(開始, 終了, ステップ)

numpy.arange([start, ]stop, [step, ]dtype=None)

>>> np.arange(3)
array([0, 1, 2])
>>> 
>>> np.arange(5)
array([0, 1, 2, 3, 4])
>>> 
>>> np.arange(2, 5)
array([2, 3, 4])
>>> 
>>> np.arange(0, 30, 5)
array([ 0,  5, 10, 15, 20, 25])
>>> 
>>> np.arange(0, 3, .5)
array([0. , 0.5, 1. , 1.5, 2. , 2.5])

linspace｜連番(開始, 終了, 要素数)

numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)

>>> np.linspace(1, 5, 5)
array([1., 2., 3., 4., 5.])
>>>  
>>> np.linspace(1, 2, 5)
array([1.  , 1.25, 1.5 , 1.75, 2.  ])

numpy.randomモジュール｜乱数

rand
- 0から1の範囲でランダムな数値を出力します。
randn
- 標準正規分布(平均値0、標準偏差1)でランダムな数値を出力します。

>>> np.random.rand()
0.9648441374742954
>>> np.random.randn()
-1.0407926498684088

>>> np.random.rand(2, 3)
array([[0.34497556, 0.82011048, 0.72948862],
       [0.22415192, 0.34738009, 0.68770817]])
>>> np.random.randn(2, 3)
array([[ 1.08734939, -0.5422097 ,  0.03434921],
       [ 0.36904612, -0.76273892,  0.1990645 ]])

rand

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

x = np.random.rand(10000)

dfx = pd.DataFrame(x)
print(dfx.describe())
#                   0
# count  10000.000000
# mean       0.496157
# std        0.288810
# min        0.000017
# 25%        0.244721
# 50%        0.489199
# 75%        0.751274
# max        0.999902

plt.hist(x, bins=100)
plt.show()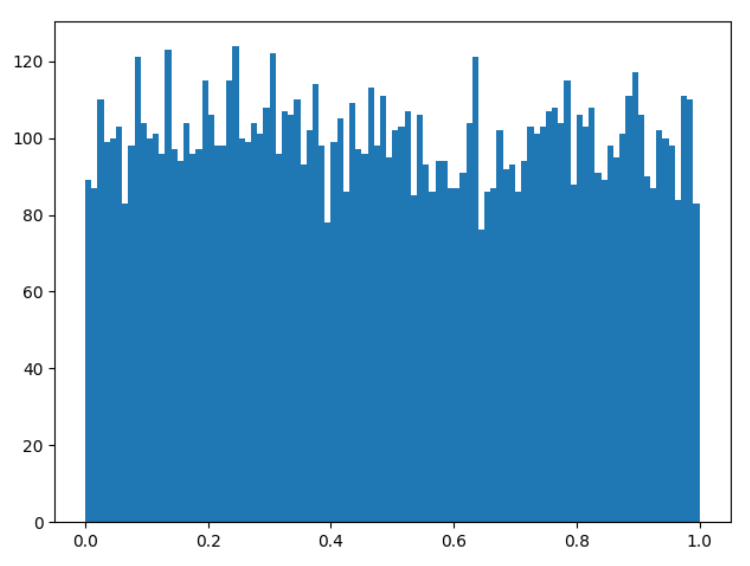

randn

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

y = np.random.randn(10000)

dfy = pd.DataFrame(y)
print(dfy.describe())
#                   0
# count  10000.000000
# mean       0.000885
# std        1.004407
# min       -3.828600
# 25%       -0.687603
# 50%        0.000938
# 75%        0.690210
# max        4.196197

plt.hist(y, bins=100)
plt.show()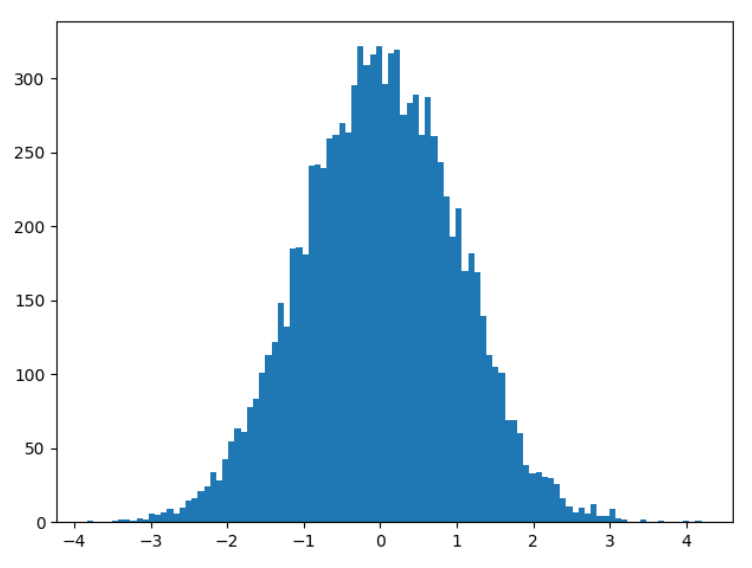

reshape｜次元を変更

一次元配列を 3×4の二次元配列に変形してみます。

>>> np.arange(12).reshape(4, 3)
array([[ 0,  1,  2],
       [ 3,  4,  5],
       [ 6,  7,  8],
       [ 9, 10, 11]])

一次元配列を 3×3×3の三次元配列に変形してみます。

>>> np.arange(27).reshape(3, 3, 3)
array([[[ 0,  1,  2],
        [ 3,  4,  5],
        [ 6,  7,  8]],

       [[ 9, 10, 11],
        [12, 13, 14],
        [15, 16, 17]],

       [[18, 19, 20],
        [21, 22, 23],
        [24, 25, 26]]])

一次元配列を 100×100 の二次元配列に変形してみます。

>>> np.arange(10000).reshape(100, 100)
array([[   0,    1,    2, ...,   97,   98,   99],
       [ 100,  101,  102, ...,  197,  198,  199],
       [ 200,  201,  202, ...,  297,  298,  299],
       ...,
       [9700, 9701, 9702, ..., 9797, 9798, 9799],
       [9800, 9801, 9802, ..., 9897, 9898, 9899],
       [9900, 9901, 9902, ..., 9997, 9998, 9999]])

ndarrayクラスの主な属性

ndim｜次元数

配列の次元数(dimension)を取得します。

>>> np.array([0, 1, 2]).ndim
1
>>> np.array([[0, 1, 2], [3, 4, 5]]).ndim
2
>>> np.array([[[0, 1, 2], [3, 4, 5]], [[6, 7, 8], [8, 9, 10]]]).ndim
3

shape｜各次元の配列サイズ

>>> np.array([0, 1, 2]).shape
(3,)
>>> np.array([0, 1, 2, 3, 4, 5]).shape
(6,)

>>> np.array([[0, 1], [3, 4], [5, 6], [7, 8]])
array([[0, 1],
       [3, 4],
       [5, 6],
       [7, 8]])
>>> np.array([[0, 1], [3, 4], [5, 6], [7, 8]]).shape
(4, 2)

>>> np.array([[0, 1, 2], [3, 4, 5]])
array([[0, 1, 2],
       [3, 4, 5]])
>>> np.array([[0, 1, 2], [3, 4, 5]]).shape
(2, 3)

>>> np.arange(24).reshape(2, 3, 4)
array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11]],

       [[12, 13, 14, 15],
        [16, 17, 18, 19],
        [20, 21, 22, 23]]])
>>> 
>>> np.arange(24).reshape(2, 3, 4).shape
(2, 3, 4)

size｜要素数

>>> np.array([0, 1, 2]).size
3
>>> np.array([0, 1, 2, 3]).size
4
>>> np.array([[0, 1, 2], [3, 4, 5]]).size
6
>>> np.array([[[0, 1, 2], [3, 4, 5]], [[6, 7, 8], [8, 9, 10]]]).size
12

dtype｜要素の型

デフォルト

[] で指定する値によって変わります。

>>> np.array([0, 1, -1])
array([ 0,  1, -1])
>>> np.array([0, 1, -1]).dtype
dtype('int64')

>>> np.array([0, 1, -1, 0.5])
array([ 0. ,  1. , -1. ,  0.5])
>>> np.array([0, 1, -1, 0.5]).dtype
dtype('float64')

32ビットの符号付き整数

>>> np.array([0, 1, -1, 0.5], dtype = 'int32')
array([ 0,  1, -1,  0], dtype=int32)
>>> np.array([0, 1, -1, 0.5], dtype = 'int32').dtype
dtype('int32')

32ビットの符号なし整数

>>> np.array([0, 1, -1, 0.5], dtype = 'uint32')
array([         0,          1, 4294967295,          0], dtype=uint32)
>>> np.array([0, 1, -1, 0.5], dtype = 'uint32').dtype
dtype('uint32')

32ビットの浮動小数点数

>>> np.array([0, 1, -1, 0.5], dtype = 'float32')
array([ 0. ,  1. , -1. ,  0.5], dtype=float32)
>>> np.array([0, 1, -1, 0.5], dtype = 'float32').dtype
dtype('float32')

真偽値

>>> np.array([0, 1, -1, 0.5], dtype = 'bool')
array([False,  True,  True,  True])
>>> np.array([0, 1, -1, 0.5], dtype = 'bool').dtype
dtype('bool')

計算

配列とスカラー

>>> np.array([[1, 2, 3], [4, 5, 6]]) + 2
array([[3, 4, 5],
       [6, 7, 8]])
>>> np.array([[1, 2, 3], [4, 5, 6]]) - 2
array([[-1,  0,  1],
       [ 2,  3,  4]])
>>> np.array([[1, 2, 3], [4, 5, 6]]) * 2
array([[ 2,  4,  6],
       [ 8, 10, 12]])
>>> np.array([[1, 2, 3], [4, 5, 6]]) / 2
array([[0.5, 1. , 1.5],
       [2. , 2.5, 3. ]])

配列と配列

>>> a = np.array([[1, 2, 3], [4, 5, 6]])
>>> b = np.array([[1, 2, 3], [4, 5, 6]])
>>> 
>>> a + b
array([[ 2,  4,  6],
       [ 8, 10, 12]])
>>> a - b
array([[0, 0, 0],
       [0, 0, 0]])

>>> a = np.array([1, 2, 3])
>>> b = np.array([[2], [3], [4]])
>>> a * b
array([[ 2,  4,  6],
       [ 3,  6,  9],
       [ 4,  8, 12]])

行列の積｜dotメソッド

行列の積を求めるには、dotメソッド を利用します。

(1×3行列)(3×1行列)

>>> a = np.array([1, 2, 3])
>>> b = np.array([[2], [3], [4]])
array([1, 2, 3])
>>> b
array([[2],
       [3],
       [4]])
>>> np.dot(a, b)
array([20])
// (1 × 2) + (2 × 3) + (3 × 4) = 2 + 6 + 12 = 20

(1×3行列)(3×2行列)

>>> a = np.array([1, 2, 3])
>>> b = np.array([[[2], [3], [4]], [[1], [1], [1]]])
>>> 
>>> a
array([1, 2, 3])
>>> b
array([[[2],
        [3],
        [4]],

       [[1],
        [1],
        [1]]])
>>> 
>>> np.dot(a, b)
array([[20],
       [ 6]])
// (1 × 2) + (2 × 3) + (3 × 4) = 2 + 6 + 12 = 20
// (1 × 1) + (2 × 1) + (3 × 1) = 1 + 2 + 3 = 6

ブロードキャスト

ブロードキャストという機能があり、要素数が足りないとき、自動で行・列を揃えてくれます。

まず、ブロードキャストを利用しないで、全ての要素に10を加えてみます。

>>> a = np.array([0, 1, 2, 3, 4, 5])
>>> b = np.array([10, 10, 10, 10, 10, 10])
>>> 
>>> a + b
array([10, 11, 12, 13, 14, 15])

次に、ブロードキャストを利用します。

>>> a = np.array([0, 1, 2, 3, 4, 5])
>>> a + 10
array([10, 11, 12, 13, 14, 15])

統計

合計

>>> np.array([[0, 1, 2], [3, 4, 5]]).sum()
15

最小値

>>> np.array([[0, 1, 2], [3, 4, 5]]).min()
0

最大値

>>> np.array([[0, 1, 2], [3, 4, 5]]).max()
5

平均値

>>> np.array([[0, 1, 2], [3, 4, 5]]).mean()
2.5

要素取得(添字とスライス)

Pythonのリストと同様の考えで以下操作ができます。

添字 で特定要素を取得
スライス で特定範囲の要素を取得

一次元配列

>>> a = np.array([0, 1, 2, 3, 4, 5])
>>> 
>>> a[0]
0
>>> a[1:3]
array([1, 2])

スライスした値を別の変数に格納した際、注意点があります。

>>> a = np.array([0, 1, 2, 3, 4, 5])
>>> a
array([0, 1, 2, 3, 4, 5])
>>> 
>>> b = a[1:4]
>>> b
array([1, 2, 3])
>>> 
>>> b[1] = 100
>>> b
array([  1, 100,   3])
>>> a
array([  0,   1, 100,   3,   4,   5])

上記のように、変数a の値も更新されます。変数a の値は更新させたくない場合、copyメソッド を利用します。

>>> a = np.array([0, 1, 2, 3, 4, 5])
>>> a
array([0, 1, 2, 3, 4, 5])
>>> 
>>> b = a[1:4].copy()
>>> b
array([1, 2, 3])
>>> 
>>> b[1] = 100
>>> b
array([  1, 100,   3])
>>> a
array([0, 1, 2, 3, 4, 5])

二次元配列

>>> a = np.arange(24).reshape(4, 6)
>>> 
>>> a
array([[ 0,  1,  2,  3,  4,  5],
       [ 6,  7,  8,  9, 10, 11],
       [12, 13, 14, 15, 16, 17],
       [18, 19, 20, 21, 22, 23]])
>>> a[0][2]
2
>>> 
>>> a
array([[ 0,  1,  2,  3,  4,  5],
       [ 6,  7,  8,  9, 10, 11],
       [12, 13, 14, 15, 16, 17],
       [18, 19, 20, 21, 22, 23]])
>>> a[:, 2:4]
array([[ 2,  3],
       [ 8,  9],
       [14, 15],
       [20, 21]])
>>> 
>>> a
array([[ 0,  1,  2,  3,  4,  5],
       [ 6,  7,  8,  9, 10, 11],
       [12, 13, 14, 15, 16, 17],
       [18, 19, 20, 21, 22, 23]])
>>> a[0:2, 2:4]
array([[2, 3],
       [8, 9]])