数式をWeb上で表示するためのマークアップ言語である「MathML」の使い方について紹介します。「MathML」は未対応のブラウザが多いので、「MathJax」というライブラリが必要です。

MathMLとは？

MathML(Mathematical Markup Language) は、HTMLタグを使用して数式をマークアップする手段を提供します。

• https://www.w3.org/Math/
• https://www.w3.org/TR/MathML3/
• https://developer.mozilla.org/ja/docs/Web/MathML

ただし、 Chrome Edge などのブラウザでは MathML に対応できていません。

• https://caniuse.com/#search=math

未対応のブラウザでも数式を表示するには、 MathJax というJavaScriptのライブラリが必要です。

• https://www.mathjax.org/
• https://github.com/mathjax/mathjax

MathJaxの導入方法

CDN 経由で MathJax を利用できます。

<script type="text/javascript" async
        src="https://cdnjs.cloudflare.com/ajax/libs/mathjax/2.7.5/MathJax.js?config=MML_SVG"></script>

configパラメーター で「どのフォーマットを利用するのか」「どのように出力するのか」といった設定を指定できます。詳しい情報は以下ページで確認できます。

• https://docs.mathjax.org/en/latest/config-files.html

主なタグ

基礎

タグ	説明
<math>	トップレベル要素
<mi>	識別子(identifier)
<mn>	数字(number)
<mo>	演算子(operator)

表、行列などに利用

タグ	説明
<mtable>	表または行列
<mtd>	表または行列のセル
<mtr>	表または行列の列

累乗、添字、積分などに利用

タグ	説明
<msub>	下付き(subscript)
<msup>	上付き(superscript)
<msubsup>	下付き上付きの組

ベクトル、総和、極限などに利用

タグ	説明
<mover>	真上付き
<munder>	真下付き
<munderover>	真下付きと真上付きの組

その他

タグ	説明
<mfenced>	括弧
<mfrac>	分数
<mrow>	グループ化された部分式
<msqrt>	平方根

利用例

どうのようにタグが利用されるのか紹介します。

加算 / 減算
( Addition / Subtraction )

$4+2+\left(10-3\right)$

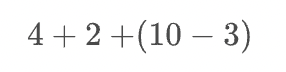
<math>
  <mn>4</mn>
  <mo>+</mo>
  <mn>2</mn>
  <mo>+</mo>
  <mfenced>
    <mrow>
      <mn>10</mn>
      <mo>-</mo>
      <mn>3</mn>
    </mrow>
  </mfenced>
</math>

乗算 / 除算
( Multiplication / Division )

$5\times 3÷2$

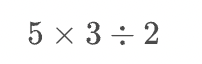
<math>
  <mn>5</mn>
  <mo>&times;</mo>
  <mn>3</mn>
  <mo>&divide;</mo>
  <mn>2</mn>
</math>

分数
( Fraction )

$\frac{x-1}{3}$

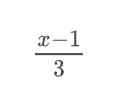
<math>
  <mfrac>
    <mrow>
      <mi>x</mi>
      <mo>-</mo>
      <mn>1</mn>
    </mrow>
    <mn>3</mn>
  </mfrac>
</math>

絶対値
( Absolute value )

$\left|-a\right|$

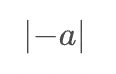
<math style="margin-bottom: 16px">
  <mo>|</mo>
  <mrow>
    <mo>-</mo>
    <mi>a</mi>
  </mrow>
  <mo>|</mo>
</math>

連立方程式
( Simultaneous equations )

$\{\begin{array}{c}2x-y=1\\ x+2y=8\end{array}$

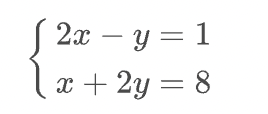
<math>
  <mo>{</mo>
  <mtable>
    <mtr>
      <mtd>
        <mn>2</mn>
        <mi>x</mi>
        <mo>-</mo>
        <mi>y</mi>
        <mo>=</mo>
        <mn>1</mn>
      </mtd>
    </mtr>
    <mtr>
      <mtd>
        <mi>x</mi>
        <mo>+</mo>
        <mn>2</mn>
        <mi>y</mi>
        <mo>=</mo>
        <mn>8</mn>
      </mtd>
    </mtr>
  </mtable>
</math>

関数f(x)
( Function )

$f\left(x\right)$

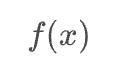
<math>
  <mi>f</mi>
  <mo>&ApplyFunction;</mo>
  <mfenced>
    <mrow>
      <mi>x</mi>
    </mrow>
  </mfenced>
</math>

累乗
( Power )

$x^3+{\left(x-1\right)}^2$

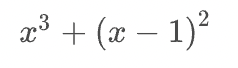
<math>
  <msup>
    <mi>x</mi>
    <mn>3</mn>
  </msup>
  <mo>+</mo>
  <msup>
    <mfenced>
      <mrow>
        <mi>x</mi>
        <mo>-</mo>
        <mn>1</mn>
      </mrow>
    </mfenced>
    <mn>2</mn>
  </msup>
</math>

対数
( Logarithm )

$y={\log }_{a}x$

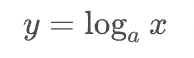
<math>
  <mi>y</mi>
  <mo>=</mo>
  <msub>
    <mi>log</mi>
    <mi>a</mi>
  </msub>
  <mi>x</mi>
</math>

平方根
( Square root )

$\sqrt{x}$

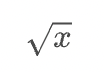
<math>
  <msqrt>
    <mi>x</mi>
  </msqrt>
</math>

三角関数
( Trigonometric function )

$\tan \theta =\frac{\sin \theta }{\cos \theta }$

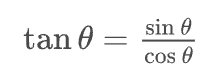
<math>
  <mi>tan</mi>
  <mi>&theta;</mi>
  <mo>=</mo>
  <mfrac>
    <mrow>
      <mi>sin</mi>
      <mi>&theta;</mi>
    </mrow>
    <mrow>
      <mi>cos</mi>
      <mi>&theta;</mi>
    </mrow>
  </mfrac>
</math>

ベクトル
( Vektor )

$\overrightarrow{v}$

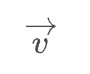
<math>
  <mover>
    <mi>v</mi>
    <mo>&RightArrow;</mo>
  </mover>
</math>

行列
( Matrix )

$\left(\begin{array}{cc}1& 2\\ -3& 4\end{array}\right)\left(\begin{array}{cc}2& 2\\ 0& 5\end{array}\right)=\left(\begin{array}{cc}2& 12\\ -6& 14\end{array}\right)$

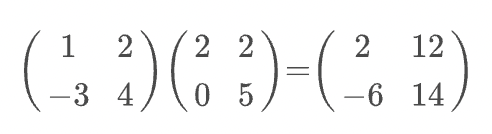
<math>
  <mfenced>
    <mtable>
      <mtr>
        <mtd>
          <mn>1</mn>
        </mtd>
        <mtd>
          <mn>2</mn>
        </mtd>
      </mtr>
      <mtr>
        <mtd>
          <mn>-3</mn>
        </mtd>
        <mtd>
          <mn>4</mn>
        </mtd>
      </mtr>
    </mtable>
  </mfenced>
  <mfenced>
    <mtable>
      <mtr>
        <mtd>
          <mn>2</mn>
        </mtd>
        <mtd>
          <mn>2</mn>
        </mtd>
      </mtr>
      <mtr>
        <mtd>
          <mn>0</mn>
        </mtd>
        <mtd>
          <mn>5</mn>
        </mtd>
      </mtr>
    </mtable>
  </mfenced>
  <mo>=</mo>
  <mfenced>
    <mtable>
      <mtr>
        <mtd>
          <mn>2</mn>
        </mtd>
        <mtd>
          <mn>12</mn>
        </mtd>
      </mtr>
      <mtr>
        <mtd>
          <mn>-6</mn>
        </mtd>
        <mtd>
          <mn>14</mn>
        </mtd>
      </mtr>
    </mtable>
  </mfenced>
</math>

総和(数列の和)
( Summation )

ギリシャ文字の Σ(シグマ) [ 総和 (Summation) の頭文字Sに相当する文字 ]を表すには ∑ を利用します。

$\sum _{i=1}^n{k}_i$

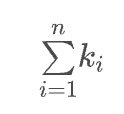
<math>
  <munderover>
    <mi>&sum;</mi>
    <mrow>
      <mi>i</mi>
      <mo>=</mo>
      <mn>1</mn>
    </mrow>
    <mi>n</mi>
  </munderover>
  <msub>
    <mi>k</mi>
    <mi>i</mi>
  </msub>
</math>

総乗(数列の積)
( Infinite product )

ギリシャ文字の Π(パイ) [ 積 (Product) の頭文字Pに相当する文字 ]を表すには ∏ を利用します。

$\prod _{i=1}^n{k}_i$

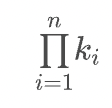
<math>
  <munderover>
    <mi>&prod;</mi>
    <mrow>
      <mi>i</mi>
      <mo>=</mo>
      <mn>1</mn>
    </mrow>
    <mi>n</mi>
  </munderover>
  <msub>
    <mi>k</mi>
    <mi>i</mi>
  </msub>
</math>

極限
( Limit )

$\underset{n\to \infty }{\lim }\frac{1}{n}=0$

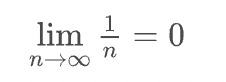
<math>
  <munder>
    <mi>lim</mi>
    <mrow>
      <mi>n</mi>
      <mo>&#x2192;</mo>
      <mi>&infin;</mi>
    </mrow>
  </munder>
  <mfrac>
    <mn>1</mn>
    <mi>n</mi>
  </mfrac>
  <mo>=</mo>
  <mn>0</mn>
</math>

微分
( Differential )

$\frac{d}{dx}{x}^3=3x^2$

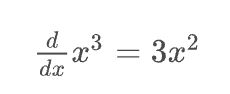
<math>
  <mfrac>
    <mrow>
      <mi>d</mi>
    </mrow>
    <mrow>
      <mi>d</mi>
      <mi>x</mi>
    </mrow>
  </mfrac>
  <msup>
    <mi>x</mi>
    <mn>3</mn>
  </msup>
  <mo>=</mo>
  <mn>3</mn>
  <msup>
    <mi>x</mi>
    <mn>2</mn>
  </msup>
</math>

偏微分
( Partial differential )

$f\left(\mathrm{x,\; y}\right)=x^2+y^2+xy$ のとき、$x$ に関する偏微分は以下のようになります。

<math>
  <mfrac>
    <mrow>
      <mo>&part;</mo>
      <mi>f</mi>
      <mo>&ApplyFunction;</mo>
      <mfenced>
        <mrow>
          <mi>x, y</mi>
        </mrow>
      </mfenced>
    </mrow>
    <mrow>
      <mo>&part;</mo>
      <mi>x</mi>
    </mrow>
  </mfrac>
  <mo>=</mo>
  <mn>2</mn>
  <mi>x</mi>
  <mo>+</mo>
  <mi>y</mi>
</math>

合成関数の微分
( Composite function )

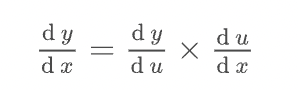
<math>
  <mfrac>
    <mrow>
      <mo>d</mo>
      <mi>y</mi>
    </mrow>
    <mrow>
      <mo>d</mo>
      <mi>x</mi>
    </mrow>
  </mfrac>
  <mo>=</mo>
  <mfrac>
    <mrow>
      <mo>d</mo>
      <mi>y</mi>
    </mrow>
    <mrow>
      <mo>d</mo>
      <mi>u</mi>
    </mrow>
  </mfrac>
  <mo>&times;</mo>
  <mfrac>
    <mrow>
      <mo>d</mo>
      <mi>u</mi>
    </mrow>
    <mrow>
      <mo>d</mo>
      <mi>x</mi>
    </mrow>
  </mfrac>
</math>

e.g.

$y={\left(\mathrm{3x}-1\right)}^8$ のとき、 $u={\mathrm{3x}-1}^{}$ として、 $\frac{dy}{dx}=8u^7\times 3=24{\left(\mathrm{3x}-1\right)}^7$ と求めることができます。

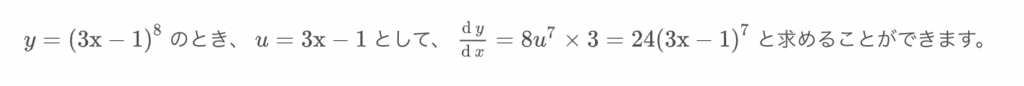
積分
( Integral )

不定積分

${\int }_{}^{}f\left(x\right)dx$

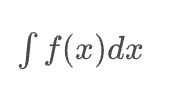
<math>
  <msubsup>
    <mo>&int;</mo>
  </msubsup>
  <mi>f</mi>
  <mo>&ApplyFunction;</mo>
  <mfenced>
    <mrow>
      <mi>x</mi>
    </mrow>
  </mfenced>
  <mi>d</mi>
  <mi>x</mi>
</math>

定積分

${\int }_{\mathrm{a}}^{b}f\left(x\right)dx$

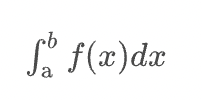
<math>
  <msubsup>
    <mo>&int;</mo>
    <mn>a</mn>
    <mi>b</mi>
  </msubsup>
  <mi>f</mi>
  <mo>&ApplyFunction;</mo>
  <mfenced>
    <mrow>
      <mi>x</mi>
    </mrow>
  </mfenced>
  <mi>d</mi>
  <mi>x</mi>
</math>

おまけ

ギリシャ文字なども、数式を書く上で必要です。

ギリシャ文字

大文字	小文字	name	名前	HTML
Α	α	alpha	アルファ	Α α
Β	β	beta	ベータ	Β β
Γ	γ	gamma	ガンマ	Γ γ
Δ	δ	delta	デルタ	Δ δ
Ε	ε	epsilon	イプシロン	Ε ε
Ζ	ζ	zeta	ゼータ	Ζ ζ
Η	η	eta	イータ	Η η
Θ	θ	theta	シータ	Θ θ
Ι	ι	iota	イオタ	Ι ι
Κ	κ	kappa	カッパ	Κ κ
Λ	λ	lambda	ラムダ	Λ λ
Μ	μ	mu	ミュー	Μ μ
Ν	ν	nu	ニュー	Ν ν
Ξ	ξ	xi	クサイ	Ξ ξ
Ο	ο	omicron	オミクロン	Ο ο
Π	π	pi	パイ	Π π
Ρ	ρ	rho	ロー	Ρ ρ
Σ	σ	sigma	シグマ	Σ σ ς
Τ	τ	tau	タウ	Τ τ
Υ	υ	upsilon	ユプシロン	Υ υ
Φ	φ	phi	ファイ	Φ φ
Χ	χ	chi	カイ	Χ χ
Ψ	ψ	psi	プサイ	Ψ ψ
Ω	ω	omega	オメガ	Ω ω

主な記号

演算子	HTML	description	説明
ⅇ	ⅇ	Natural number	ネイピア数、自然対数の底
ⅈ	ⅈ	Imaginary i	虚数
∞	∞	Infinity	無限

主な演算子

演算子	HTML	description	説明
≥	≥	Greater than or equal to	以上
>	>	Greater than	より大きい
≤	≤	Less than or equal to	以下
<	&lt;	Less than	より小さい
≠	&ne;	Not equal to	等しくない
±	&pm;	Plus or minus
∈	&#x2208;	element of	属する
∉	&#x2209;	not an element of	属さない
⊂	&#x2282;	subset of	部分集合
⊄	&#x2284;	not a subset of
∩	&#x2229;	intersection	集合積
∪	&#x222A;	union	集合和

https://www.w3.org/TR/MathML3/appendixc.html